11 The t-Test
Parametric test of group differences. It is used when:
- There is a single predictor/independent variable (IV);
- The predictor/independent variable is measured on a nominal scale and can have only two values;
- The criterion/dependent variable is measured on an interval or ratio scale.
11.1 Independent Samples t-Test
Used when the observations collected under one treatment condition are not related to the observations collected under the other treatment condition. For example, the independent samples t-Test is used when randomly selected subjects are exposed to two different experimental conditions (IV) and we want to know if the two groups are or are not different on some characteristic (DV).
The following assumptions must be met to use the independent samples t-Test:
- Normally distributed data.
- Randomly selected samples;
- Samples are independent;
Data normality can be verified by looking at the distribution of the data (histograms) or through a test of normality. F or Levene’s tests can be used to test equality of variances.
The test computes the probability of error for rejecting the null hypothesis of no difference between the two means. Therefore, the p-value reported by the t-Test represents the probability of being wrong in accepting the research hypothesis (alternative hypothesis) that a difference in means exists.
An example: consider studying the differences in height between males and females of the homo sapiens species. We measure 100 individuals, 50 females (F) and 50 males (M). An excerpt of the height measurement data is presented in Table 11.1.
Table 11.1: Excerpt from the height data set
| Gender | Height |
|---|---|
| F | 67 |
| F | 67 |
| F | 60 |
| M | 72 |
| M | 71 |
| M | 67 |
The null hypothesis (H0): In the population there is no difference between male and female heights.
The first step in data analysis is to familiarize oneself with the data. So, let’s take a look at the some summary statistics.
Gender Height
F:50 Min. :60.0
M:50 1st Qu.:67.0
Median :69.0
Mean :69.4
3rd Qu.:72.2
Max. :79.0 11.1.1 Testing Assumption of Normality
As an example, we will work through the most common options to test the normality of a dataset.
Distributions
Figure 11.1: Histogram of male and female heights
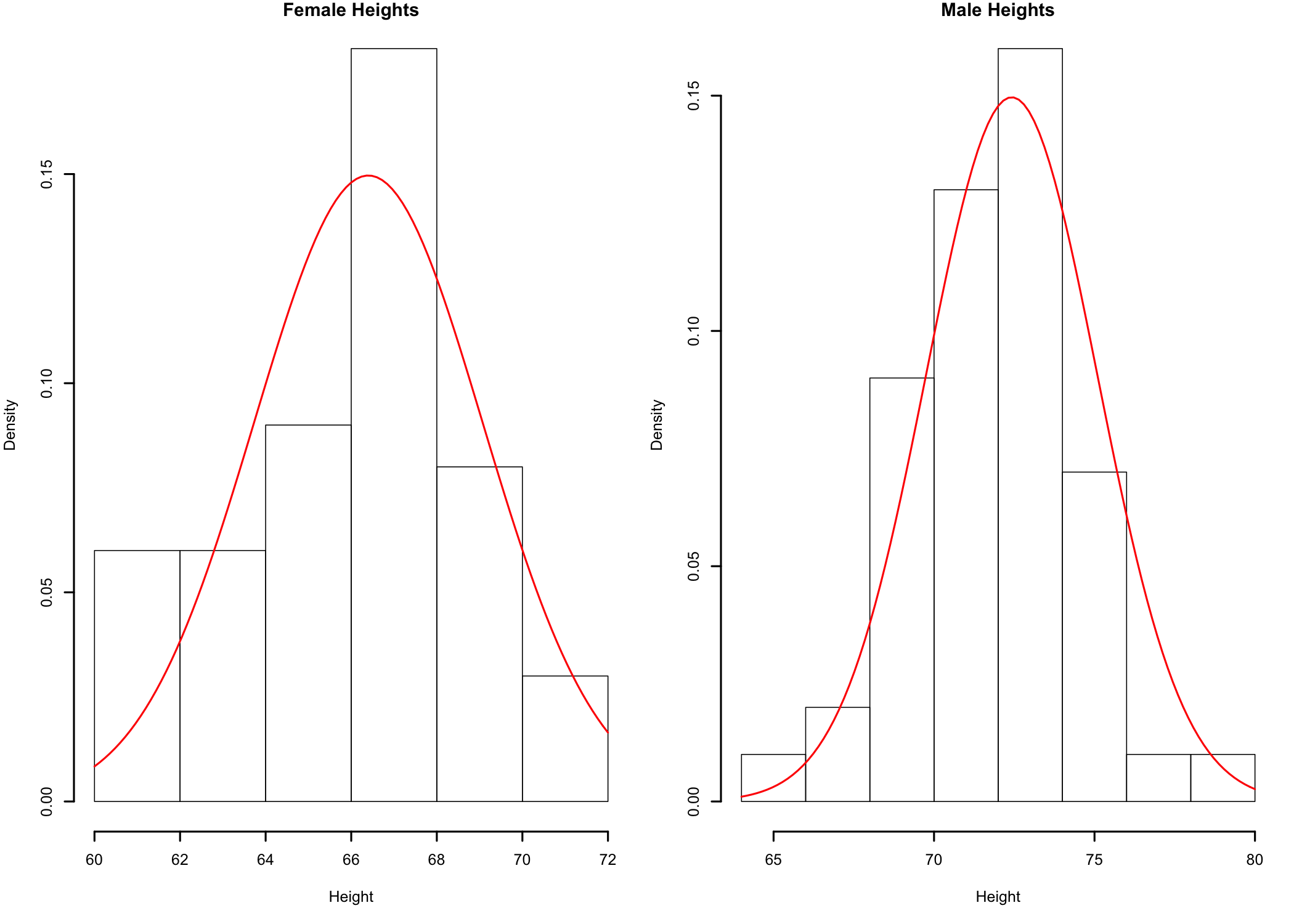
Based on the histogram plots (Figure 11.1) the data seems to be relatively close to a bell-shaped distribution90 The histograms for Males and Females may look different because of possible differences between the number of bars used to represent the data. This is due to the way R computes the number of bins to use for data representation of a data set.. In this case, while the resemblance to a bell shape may be more difficult to observe, it is because of the small number of data points available for analysis. The more data points in the sample, if the sample distribution is close to the normal distribution, the closer the histogram would be to the bell-shaped curve of the normal distribution. While the visual checks are fine, let’s take a closer look at sample data normality.
qq-Plots
Figure 11.2: qq-plots of height data by gender.
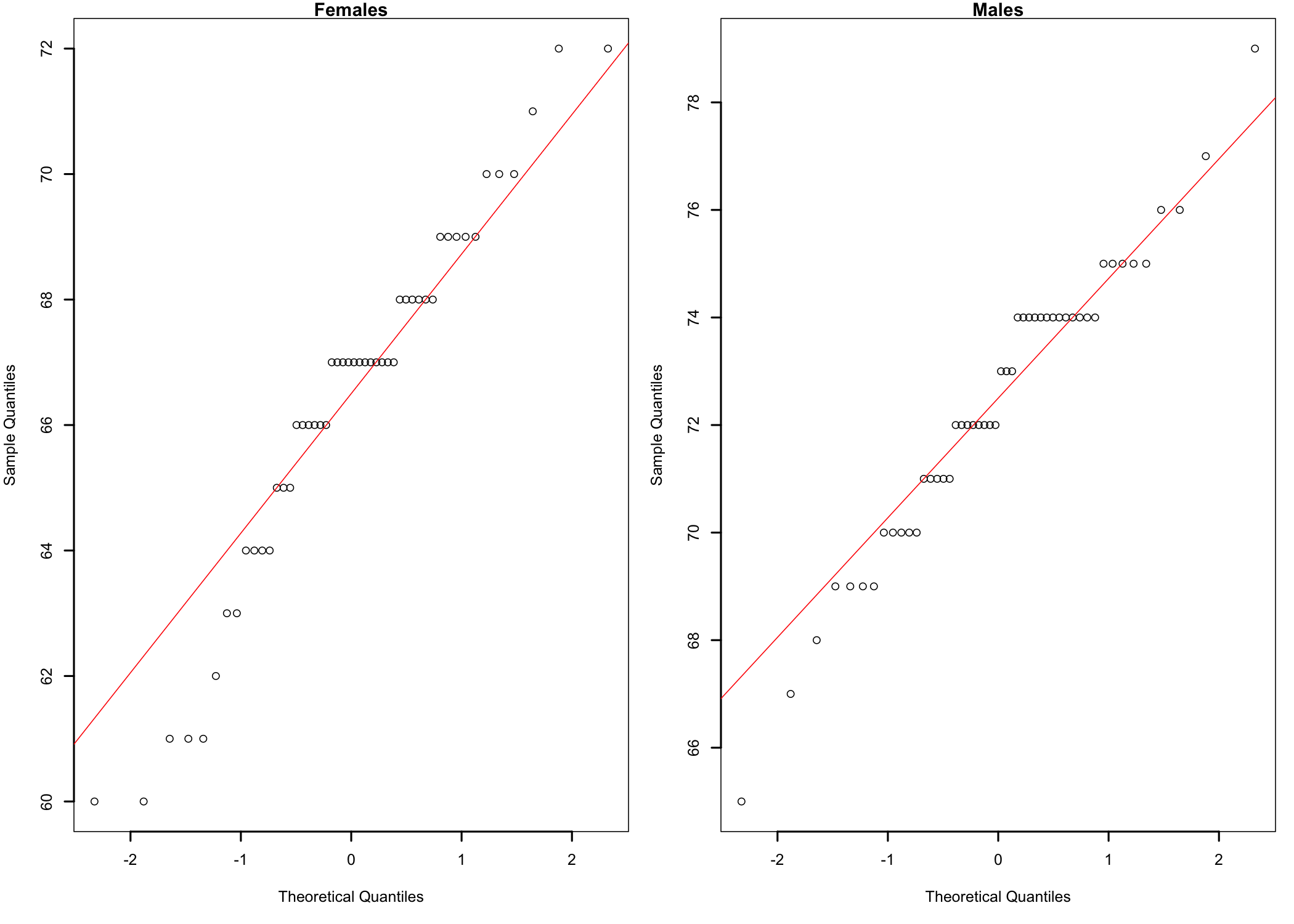
As Figure 11.2 shows, the data points form a fairly straight line for both males and females, which suggests the conclusion that the sample data for the two groups is normally distributed. The slight S-shaped curve is an indication of some departures from normality, but a visual inspection comparing the data points curves with the red straight diagonal lines suggests that these departures are not significant. Nevertheless, to be sure, let’s not rely on visual clues alone.
Skewness and Kurtosis
Table 11.2: Skewness and kurtosis of height data
| Skewness | Kurtosis | |
|---|---|---|
| Females | -0.4309 | 2.828 |
| Males | -0.3150 | 3.284 |
The data in Table 11.2 shows that for females the data is slightly skewed to the left and playtkurtic (kurtosis < 3). The sample of males shows a similar situation. While numbers offer a bit more detail than visual representation, let’s go a step further and test data normality using a more specific statistical test.
Shapiro-Wilk Test
Shapiro-Wilk normality test
data: my.F
W = 0.96, p-value = 0.06
Shapiro-Wilk normality test
data: my.M
W = 0.97, p-value = 0.2A p-value > 0.05 indicates that the null hypothesis cannot be rejected and therefore it should be concluded that the samples follow a normal distribution.
11.1.2 The t-Test
Welch Two Sample t-test
data: Height by Gender
t = -11, df = 97, p-value <2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-7.13 -4.91
sample estimates:
mean in group F mean in group M
66.40 72.42 The output shows the probability p (p-value) that the t statistics would be this large or larger in absolute value (without the - sign) if the null hypothesis is true. For this analysis the value of p is so small91 The value of the p-value is so small that R considers it, for the purpose of this test, indistinguishable from 0 and thus represented as 2.2e-16 (0.00000000000000022). R can represent smaller numbers, but for all intents and purposes, unless one needs to work with very, very small p-values, this value can be effectively considered equal to 0. that there is practically no chance that the null hypothesis is true. Therefore, the conclusion is that, on average, there is a significant difference in height between males and females.
Finally, here is an example of how to write up the results in a publication.
An independent-samples t-Test used to analyze the data revealed a significant difference in height between males and females, t(97.193) = -10.765; p < 0.001. The sample means show that males are significantly taller (mean = 72.42) than females (mean = 66.40).
11.2 Paired Samples t-Test
The paired-samples t-Test is used when the observation collected from one group is related in some way to the corresponding observation in the second group. Some examples of studies where this test would be appropriate:
- A study using repeated measures in which case some characteristic is measured for the same participants before and after a treatment. In this case, because the participants are the same, an observation before the treatment will have a corresponding observation after the treatment, with the correspondence being provided by the participant.
- A variant of the above is a pretest-postest study, where there is a test given to the participants before the intervention, and then another test is given after the intervention.
- A study in which the participants are assigned to the treatment groups using some type of matching procedure or process. That is, one participant is exposed to one of the experimental conditions while another participant, selected using a matching procedure is exposed to the other experimental treatment.
- A study in which each participant is exposed to both treatment conditions.
Assumptions underlying paired-samples t-test:
- DV - interval or ratio.
- IV - nominal with only two categories.
- Observations should be paired in some meaningful way.
- Independent observations, a participant’s score in one treatment should not be affected by anther participant’s score(s).
- Random sampling drawn from population.
- Normal distribution of difference scores.
- Homogeneity of variance.
Paired-samples t-tests problems:
- The designs that utilize this type of t-test are many times fairly weak.
- The experiment can have many confounding variables, such as the order of treatments for a study in which each participant is exposed to both treatment conditions, in which case it could be difficult to determine if the outcomes are because of the treatment conditions themselves, due to the order of treatments, or a combination of both.
- Repeated measures tests can also show significant confounding, especially for those that span a significant amount of time (e.g., a semester) over which things that happen outside the treatment conditions can influence the outcome.